Los números reales pueden ser ubicados en una recta. Por ejemplo, podemos ubicar el 3 (en azul) y el -2 (en rojo):
![]()
Cuando se multiplica un número por -1, lo que se hace es girarlo 180º en el sentido contrario a las agujas del reloj.
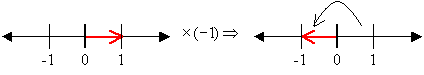
Un número negativo multiplicado por si mismo da como resultado uno positivo
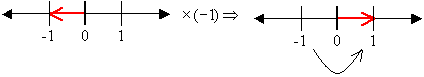
Un número complejo se define del siguiente modo:
![]()
donde a y b son dos números reales, y j es la unidad imaginaria.
Los números complejos se representan en un plano. Por ejemplo, el número 3+2*j (color azul) se representa así
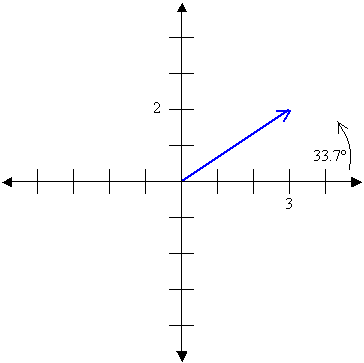
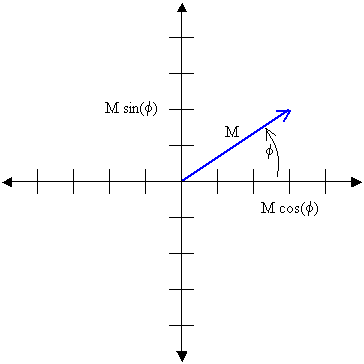
El eje horizontal es el eje de los reales, y el vertical es el de los imaginarios. El número tiene un largo (o módulo) y un ángulo de inclinación, el que se mide respecto al eje real, y que es de 33,7º en este caso. Un número complejo puede escribirse en forma cartesiana o polar
Forma cartesiana
![]()
Forma polar
![]()
Donde M es el módulo y a es el ángulo de inclinación.
La unidad imaginaria j se define como un número de módulo 1 y de ángulo 90º
![]()
Los números reales positivos tienen ángulo 0º y los negativos ángulo 180º
Para sumar dos números complejos se suman sus respectivas partes reales e imaginarias
![]()
Para multiplicar dos números complejos se multiplican sus módulos y se suman sus ángulos.
![]()
Luego:
![]()
Para transformar de forma a polar a cartesiana se hace lo siguiente:
![]()
Representación Fasorial
Si se tiene un conjunto de funciones sinusoidales de igual frecuencia angular w (omega):
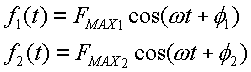
se puede asociar a cada una de ellas un número complejo llamado fasor, que se define a continuación:
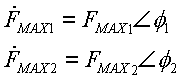
cumpliéndose la siguiente relación entre ambos:
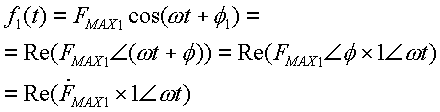
Se puede rescribir el fasor de modo que su módulo sea el valor RMS de la función
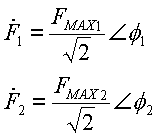
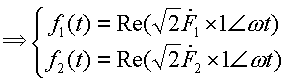
Luego, tanto la amplitud FMAX como el ángulo de fase fi de la función sinusoidal forman parte del fasor. Si se tiene un fasor y se conoce la frecuencia angular w, siempre es posible reconstruir la función original.
Se cumplen las siguientes relaciones entre sinusoides de la misma frecuencia angular w y sus respectivos fasores
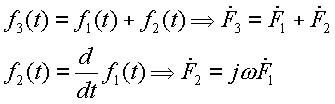
Esto hace que los fasores sean una herramienta muy útil para trabajar matemáticamente con sinusoides de la misma frecuencia.